— 6 —

• The replication crisis in the statistical sciences
  • A minimal primer on p-values
• Propensity of false positives
  • Half of published papers are false?
• Perspectives on false discovery
  • Popper and the soft sciences
  • Researcher degrees of freedom
  • Garden of the forking paths
  • Goodhart’s law
• Notes
• References

The previous chapter covered the theoretical dangers of data-dependent analyses and test set reuse. When scientists evaluate models that depend on the data, the reported numbers can be wrong. This applies equally to test sets in machine learning as it does to common statistical analyses. In this chapter we take a closer look at the empirical reality of the problem. We start with the so-called replication crisis that has long gripped applied statistical sciences. The discussion here isn’t directly about machine learning. Nevertheless, it will teach us general lessons about what makes statistical analysis vulnerable. These insights apply also to the problem of replication in machine learning, which is the topic of the next chapter.

The replication crisis in the statistical sciences

Statistical methodology is the foundation of empirical work in many scientific fields including psychology and social psychology, medicine and the biomedical sciences, economics, neuroscience, and political science. The replication crisis refers to the empirical reality—past and present—that many scientific findings fail to replicate. Simply put, failure to replicate means that a research team tries to show the finding of a previous study in another setting but doesn’t succeed.

The problem gained widespread attention a couple of decades ago and has been a topic of debate stretching beyond academic circles. Methodologically, the replication crisis is closely tied to the statistical tradition of null hypothesis significance testing. To understand the debate, it’s therefore helpful to develop a high-level understanding of hypothesis testing. At the technical level, this won’t add anything we haven’t seen already, but there is a bit of new terminology.

Why even bother with p-values and hypothesis testing at this point? You’d be right to ask. Why should you wrap your head around what seem like a statistical relic that’s caused so much confusion? If p-values were the sole culprit of the replication crisis—nothing more than a grave methodological mistake—and there was an easy fix by swapping them out for a better statistic, I’d say you probably shouldn’t. But the replication crisis that unfolded around null hypothesis testing reveals something more fundamental about the use of statistics under competitive pressure. It’s this broader insight that we’re working towards, which will transfer to machine learning research as well.

A minimal primer on p-values

The example of Freedman’s paradox in the previous chapter prepared us well. But let’s start from scratch. The main fact we need is that p-values are tail probabilities of the null model. The null model is the data-generating distribution under the null hypothesis. By convention, the null hypothesis captures a situation of no signal, e.g., the treatment has no effect. In this case, a scientist should not report a finding.

To give a formal example, a simple null model to think of is a fair coin taking values in \{-1,1\} with mean 0, representing the situation that a treatment effect is 0. If we take n samples from the null model and average them out, we get a value that concentrates around 0. From Chernoff’s bound in Chapter 3, we know that the tail probability p of seeing a value \epsilon>0 or greater is at most p \le \exp(-\epsilon^2 n/2)\,. This tail probability is the p-value. The sample average in this example is called the test statistic in the language of null hypothesis testing. The value \epsilon corresponds to the observed value of the test statistic. The larger the observed test statistic, the smaller the p-value.

Although this is just one example, many commonly used tests have subgaussian tails of the form p=\exp(-c\epsilon^2 n) where c>0 is some constant. Any such tail expression is a just different way to write \epsilon^2 n. To say that a p-value is small is therefore equivalent to saying that n \gg 1/\epsilon^2\,. This is the fundamental lesson from Chapter 3: Sample size requirements scale quadratically in the inverse of the difference that we’re trying to detect. A p-value is small if this sample size requirement is met. That’s all. There’s nothing new here other than terminology.

When you think of p-values as tail probabilities, an important issue stands out right away. Knowing both \epsilon and n may be more helpful than knowing p alone. The reason is that the p-value conflates two situations:

• small effect, large sample
• large effect, small sample

As a scientist, you probably shouldn’t be indifferent between the two. You might prefer a large effect shown with a small sample over a tiny effect shown with a vast sample. But from seeing the p-value alone, you can’t decide which case it is. Large datasets make p-values small, even if there is no large effect. Don’t mistake small p-values for large effects.

Null hypothesis tests either reject the null hypothesis or they don’t. The decision criterion for rejection is that the p-value is below a certain threshold \alpha called significance level. Statistical tradition enshrined a significance level of \alpha=0.05. If the p-value comes out below the significance level of 0.05, scientists will report a significant finding. In the common caricature of the scientific process, a significant p-value means that the scientist gets to publish the finding as a scientific discovery. In reality, there’s of course a lot more going on, but the caricature is helpful for the sake of argument.

Keep in mind, a significant p-value says nothing more than that the sample size requirements are met for the kind of analysis you claim to be doing. To think of this condition on its own as a scientific discovery is unjustified.

Call a rejected null hypothesis a positive and a null hypothesis that stands a negative. Rejecting a null hypothesis that’s true is a false positive, we incorrectly declare discovery. Of course, we can always avoid false discovery by never rejecting a null hypothesis. But we also want to reject a false null hypothesis with high probability. This requires specifying an alternative hypothesis H_1. In contrast with the null hypothesis (H_0), the alternative hypothesis H_1 captures the case of there is signal in the data, e.g., the treatment is effective.

Once we have an alternative hypothesis, we can talk about the probability of rejecting the null hypothesis when the alternative is true. This quantity is called the power of the test: \text{power} = \mathop{\mathrm{\mathbb P}}\{\text{reject null } H_0 \mid \text{alternative } H_1 \text{ true}\} By convention, statisticians recommend tests with power at least 0.8. In the language of prediction from Chapter 2, statistical power is the same as the true positive rate of the test. It’s the probability of declaring a positive given that we have a positive. Recall that this is the same as one minus the false negative rate.

Propensity of false positives

At this point there are several meta studies about the replicability of empirical findings. In a major effort, published in 2015, researchers conducted replication attempts of 100 experimental and observational studies from three major psychology journals.¹ The studies all used sufficiently high-powered tests.

The results of the meta study are sobering. Whereas almost all of the original studies reported significant results (p < .05), only 36% of the replication attempts yielded p-values below the 0.05 level. Effect sizes also didn’t fare too well. Only 47% of the original effect sizes were in the 95% confidence interval of the replicated effect size. Put differently, less than half of the published papers replicated.

Scatter plots are a nice way to visualize such replication studies. On the x-axis we have the original effect size. On the y-axis, we look at the replicated effect. The main diagonal corresponds to perfect replication. Most studies fall below the main diagonal, implying that the replicated effect size is smaller than the original. At the same time, there is a strong positive correlation between effect sizes in the original study and the replicated result.

Half of published papers are false?

Long before the meta study mentioned above, the epidemiologist John Ioannidis made a thought-provoking back of the envelope calculation suggesting that most published papers are wrong.

The argument is simple and has aged well. What we need to start is a number p_{\text{true}} corresponding to the pre-study probability that a random statement in a community is true. This probability must come from some kind of story about what statements the community studies. A more ambitious community might have a smaller value, a more incremental community might have a larger value. So, we’re going to pull this number out of the hat eventually.

Scientists run analyses that either output positive or negative. If an analysis is positive, the scientist publishes the statement as a discovery. The true positive rate corresponds to the probability that the scientist publishes a true statement:

• True positive rate (TPR): \mathop{\mathrm{\mathbb P}}\{\text{positive} \mid \text{true}\} = 1 - \beta

As we observed above, this is the same concept as power in the context of hypothesis testing. The false positive rate is the probability that the scientist publishes a false result:

• False positive rate (FPR): \mathop{\mathrm{\mathbb P}}\{\text{positive} \mid \text{false}\} = \alpha

Now, consider the probability \mathop{\mathrm{\mathbb P}}\{\text{true} \mid \text{positive}\} corresponding to the event that we actually have a true finding given that we declared a finding? This is what’s called precision or positive predictive value (PPV) in the context of prediction. In the context of scientific discovery, we can interpret it as the post-study probability of a true statement. It tells us what the fraction of true statements is among published results.

A calculation using Bayes’ rule reveals a standard textbook formula that relates all these quantities: \text{PPV} = \frac{\text{TPR} \, p_{\text{true}}}{\text{TPR} \, p_{\text{true}} + \text{FPR} \, (1 - p_{\text{true}})} Plugging in the parameters, \text{PPV} = \frac{(1 - \beta)p_{\text{true}}}{(1 - \beta)p_{\text{true}} + \alpha(1 - p_{\text{true}})}\,. In particular, \text{PPV} \ge 1/2 if (1 - \beta)p_{\text{true}} \ge \alpha(1 - p_{\text{true}})\,. If \text{PPV} < 1/2, Ioannidis says most published findings are wrong.

Let’s fill in reasonable values for \alpha,\beta, and the baseline rate of true statements:

• Significance level \alpha=0.05, commanded by statistical tradition.
• Power 1-\beta=0.8, considered to be reasonable.
• Baseline rate p_{\text{true}}=0.1. This is a guess.

With these settings, we get \text{PPV}=0.64, a value just a bit larger than 1/2. Most published research findings aren’t wrong yet.

In order to get a value below 1/2, Ioannidis considers the role of publication bias. Formally, publication bias corresponds to a certain probability u that a result gets published regardless of its truth value due to pressure to publish. This changes TPR and FPR as follows:

• \text{TPR} = P(\text{positive} \mid \text{true}) = 1 - \beta + u\beta = 1 - (1 - u)\beta
• \text{FPR} = P(\text{positive} \mid \text{false}) = \alpha + u(1 - \alpha) = (1 - u)\alpha + u

Publication bias actually increases the true positive rate. After all, more things get published, hence also the true ones. This is good. But the big issue is with the adjustment to the false positive rate that basically jumps up by an additive u.

Plugging in default values and the choice of u=0.05, again a guess, we have \text{PPV} = 0.48\,. Now we can say at last that more than half of published findings are probably false.

Ioannidis’ argument sparked a healthy debate. Several responses to the paper pointed out some obvious and some not so obvious issues with the setup and the assumptions.² Ultimately, though, many found Ioannidis’ claim plausible. In particular, the replication study above—published ten years later—supports the claim. If nothing else, Ioannidis sparked an important conversation in the statistical sciences that’s continuing to this day.

Perspectives on false discovery

If we accept the propensity of false discovery in the statistical sciences as an empirical fact, the next question is: Where do false discoveries come from? Why are there so many? Answers to these questions go back decades.

Popper and the soft sciences

Paul Meehl is a towering figure in statistics and psychology. He’s best known as a sharp and vocal proponent of statistical methods over human decision making in clinical settings, a scientific program he pursued for more than four decades.³ His work had a profound influence generations of scientists. Among those Meehl influenced is the psychologist Daniel Kahneman, whose scientific legacy centers on biases in human decision making.

Meehl’s work on statistics ran into questions about how we come to know things from data, and how statistical data analysis relates to scientific inquiry more broadly. For much of his life, Meehl nurtured a deep interest in the philosophy of science, writing prolifically about the subject. He also ran a center of philosophy of science at the University of Minnesota that drew famous visitors like Paul Feyerabend, the iconoclast of anything goes.

In the 1970s, Meehl was rather infatuated, so he said, with Popper’s philosophy of science and, in particular, the idea that science advances through falsification. Popper held that science can’t verify, but it can falsify the predictions that a theory makes. Science advances by developing theories incrementally that withstand repeated attempts at falsification.

At first glance, p-values seem to fit Popper’s ideas like a glove. What would a rejected null hypothesis be other than a falsification of something? Meehl recognized a severe limitation that p-values have, especially in the soft sciences. Although Meehl’s argument leans on Popper, it remains independently relevant today. To make the argument, Meehl invokes Popper’s principle of falsification (modus tollens):

• Suppose theory T implies a falsifiable condition C.
• If we can show that C is false, we refute T.

The gist of Meehl’s argument is that any theory usually only implies an observable condition if additional auxiliary conditions hold. These auxiliary conditions include assumptions that specific lab conditions are met, that various measurement devices work as intended, that subjects weren’t primed, biased or poorly chosen, and so forth.

Put more formally, in the empirical sciences we always have implications of the form (T \land A) \rightarrow C, where A is a sequence of assumptions. If the theory is true and the auxiliary conditions hold, we get a falsifiable prediction C.

Logically, if we refute C, we just get the proposition \neg T \lor \neg A, that is, either the theory failed or the auxiliary conditions failed (or both). Meehl argues that, therefore, null hypothesis tests in the soft sciences rarely execute a successful modus tollens against the theory. Rather we end up wondering if we perhaps only invalidated the auxiliary conditions that the test relies on. A scientist who declares a theory refuted from a rejected null hypothesis might’ve just discovered a quirk in the experiment. This, at least, is a simplified account of Meehl’s deeper argument.

Researcher degrees of freedom

In 2011, Simmons, Nelson, and Simonsohn wrote an article called False-Positive Psychology: Undisclosed Flexibility in Data Collection and Analysis Allows Presenting Anything as Significant that would shape the conversation about the replication crisis. The trio claimed:

In fact, it is unacceptably easy to publish “statistically significant” evidence consistent with any hypothesis. The culprit is a construct we refer to as researcher degrees of freedom.⁴

Researcher degrees of freedom refers to the many choices a researcher makes—often subconsciously or on autopilot—during the routine research process that can lead to false positive findings.

To give an example, imagine a treatment that you suspect from your domain knowledge works best within a certain demographic. So you choose to run an experiment in a city that matches the demographic you have in mind. You include variables you think are relevant, while excluding a whole slew of variables you could’ve included. The inclusion and exclusion may be based on prior interactions with the data, or it may happen in your head. You set out to run an experiment for three months. But the numbers look good after two months, so you stop early. Once you have the data, you do exploratory data analysis to see what’s going on. You realize that one column is particularly noisy, and so you drop it. Other columns need to be normalized in certain ways and the data suggest a good way of doing it. Finally, you run a few different statistical methods to see which works best.

Each of these is an example of researcher degrees of freedom. Many of them may end up being undisclosed and unaccounted for in the final paper.

Researcher degrees of freedom often blur into accusations of p-hacking—tweaking statistical analyses until a significant p-value pops. Fishing, cherry picking, data dredging, HARKing (“Hypothesizing After the Results are Known”) are a few other common slurs with similar meanings. These terms portray a motivated scientist who does whatever questionable practice it takes to clear the publication bar.

One way to avoid p-hacking is pre-registration. Pre-registration requires that you fully and precisely specify the exact experimental design, data collection procedure, and statistical analysis ahead of time. You publicly commit to a pre-registration plan—there are services, such as the Open Science Framework, to do so. Reviewers can then check if you stuck to the plan. Pre-registration is increasingly common in many scientific fields. The Open Science Framework surpassed 100,000 registrations in 2022.⁵

Not long after writing false positive psychology, the trio founded a blog, Data Colada, devoted to the replication crisis. The blog has since covered numerous high profile retractions of scientific papers. Several of them include instances of fraud.

But fraud is likely not primary driver of the scientific crisis, and it’s not the problem we’re concerned with here. The focus is on how science succeeds or fails under normal behavior. Competition among researchers, for example, is normal behavior. Researchers, being sensitive to incentives, find creative ways to navigate the system. Scientists are not exempt from human cognitive and behavioral biases. Confirmation bias—the inclination to see what you believe is true—is particularly common among scientists.

Garden of the forking paths

Terms like p-hacking have a decidedly negative connotation that borders on an accusation of fraud.

But trying out multiple things is not wrong so long as we correctly adjust for it. Multiple hypothesis testing is a venerable field of statistics devoted to the problem. The most basic correction from the theory of multiple hypothesis testing is called Bonferroni correction. It says that if you compute k statistics on a dataset, each giving you a p-value, then you need to multiply each p-value by the factor k. So, the value p goes to kp. Only if kp<0.05 can you claim that you meet the 0.05 significance level. Formally, Bonferroni is just the union bound. Remember that p-values are tail probabilities. So, to bound the probability that not a single one out of k deviations is large, the union bound suggests that you multiply the tails by a factor k.

Disappointed? You’re not alone. Researchers love to avoid Bonferroni for the obvious reason that it makes p-values quite a bit larger. There are more sophisticated adjustments, like the Benjamini-Hochberg procedure, that can provide some relief. However, the basic fact remains: Adjusting for multiple comparisons is painful.

Yet, there is a bigger problem, still. In most cases, it’s hard to even say what the actual number of comparisons was. Keep in mind that an adaptive analyst (Chapter 5) making k data-dependent comparisons spans a tree of 2^k possible comparisons. These possibilities are so-called implicit comparisons. They happen, but you don’t see them. Still you should adjust for them and that would often entail a huge penalty on your p-values.

In the context of the replication crisis, Gelman and Loken⁶ drew attention this problem they called garden of the forking paths:

Our main point in the present article is that it is possible to have multiple potential comparisons (that is, a data analysis whose details are highly contingent on data, invalidating published p-values) without the researcher performing any conscious procedure of fishing through the data or explicitly examining multiple comparisons.⁷

Gelman and Loken argue that science is fundamentally adaptive. Many design choices are data dependent. We simply don’t know exactly what to do ahead of time. What data to include or exclude, how to clean data, how to filter data, these practices may not feel like “fishing” or “hacking” to researchers.

By design, pre-registration forces the analysis to be non-adaptive, depriving researchers of their degrees of freedom, and eliminating the possibility of implicit comparisons. It’s often safe, but is it too constraining? Gelman and Loken argue:

At the same time, we do not want demands of statistical purity to strait-jacket our science. The most valuable statistical analyses often arise only after an iterative process involving the data (see, e.g., Tukey, 1980, and Box, 1997).⁸

This quote nods to the prominent statisticians John Tukey and George Box who both advocated for what we called adaptivity in the previous chapter, i.e., allowing for flexibility and iterative progress in statistical practice.⁹ Incremental improvements are important.

The last point resonates with machine learning practice. The idea of pre-registration is a non-starter in machine learning, where incremental dataset reuse is at the core of all practice. Researcher degrees of freedom are a key culprit of the crisis and machine learning has no way to limit them. Shouldn’t we then expect a replication crisis in machine learning research, too? This is the topic of the next chapter.

Goodhart’s law

Abstractly speaking, p-values are statistics that serve a control purpose. Academic communities use them to aid consequential decisions about which papers get accepted into prestigious journals. Such decisions in turn influence who gets desirable jobs, grants, and access to opportunities in academia. As a result, academics inevitably put competitive pressure on p-values in the sense that all the incentives point toward getting smaller p-values, and especially crossing the 0.05 threshold. Academics are resourceful and will do what it takes, typically within the parameters of ethical conduct, to cross the threshold.

In 1984, macroeconomist Charles Goodhart warned:

Any observed statistical regularity will tend to collapse once pressure is placed upon it for control purposes.¹⁰

The warning has since become an empirical law named after Goodhart. Once you use a statistical criterion as a decision threshold, be it for financial regulation, government benefits, college admissions, or journal acceptance, people will change their behavior so as to cross the threshold. What follows is that the statistical regularities you previously observed will change.

This change in behavior is often denounced as gaming the threshold, but it may also include sincere attempts to meet the requirements. Either way, whatever statistical patterns held before break down as a result of this change in behavior.

Goodhart’s law has a beautifully simple empirical test: Check for a discontinuity in the statistic around the decision threshold. Goodhart’s law predicts that a discontinuity exist due to the competitive pressure to cross the threshold. As a result we would expect too much probability mass just above or below the threshold depending on which case is desirable.

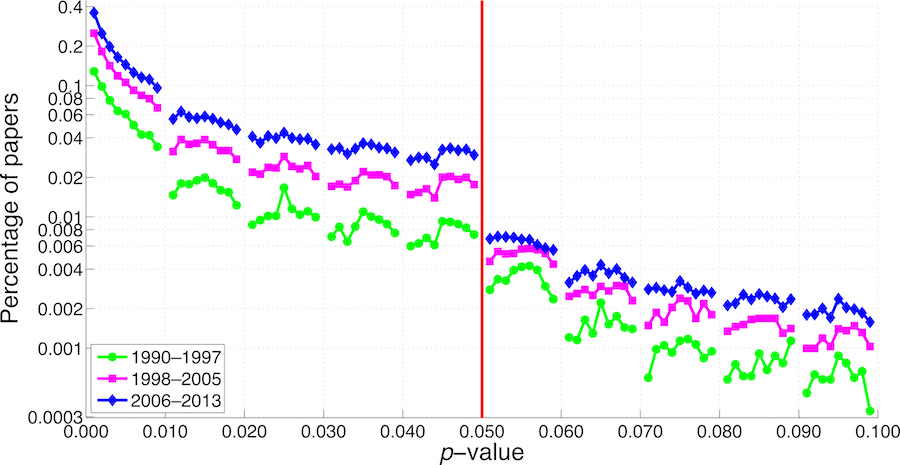
As predicted, p-values exhibit such a discontinuity just around 0.05. But there’s nothing special about p-values here. Goodhart’s law predicts that any statistic will meet the same fate as p-values. Indeed, the literature is littered with good examples of Goodhart’s law.

There is no reason to believe that Goodhart’s law wouldn’t apply to accuracy on ImageNet and other benchmark numbers. If we take improvements in benchmark performance as a criterion for paper acceptance, we are using a statistic for control purposes. The law applies.

Notes

Historical background.

The methodological debate about hypothesis testing in statistics is about a century old. Gigerenzer et al.¹¹ discuss the early historical divide between Fisherian and Neyman-Pearson style hypothesis testing and argue that modern statistics, particularly in psychology and the social sciences, often conflates these two approaches into a hybrid model that lacks coherence. This hybridization—where researchers calculate p-values (Fisherian) but also interpret them in terms of rejecting or accepting hypotheses (Neyman-Pearson)—leads to misunderstandings and misuse of statistical methods. In a 1945 article that remains relevant, Herb Simon argued that binary hypothesis tests are a poor basis for decision making and advocated for a more comprehensive decision making framework.¹²

Critiques of p-values were plentiful already more than half a century ago. A book called The Significance Test Controversy: A Reader, edited in 1970, contains thirty articles that almost all condemn the practice of null hypothesis testing.¹³ Contained in the collection is Meehl’s 1967 article on theory-testing¹⁴ that predates his 1978 tabular asterisks¹⁵. There’s more Meehl wrote on the topic. See, for example, his 1997 book chapter The problem is epistemology, not statistics: Replace significance tests by confidence intervals and quantify accuracy of risky numerical predictions.¹⁶ The chapter gives an updated view of his argument.

For additional historical background and references, see Cohen’s 1994 polemic The earth is round (p<.05).

Perspectives on the crisis.

The statistical replication crisis has been covered extensively. Apart from the articles by Ioannidis¹⁷, Simmons, Nelson, Simonsohn¹⁸, and Gelman and Loken¹⁹, that I covered above, there are many other high-level perspectives. See, for example, Stark’s Cargo-cult statistics and scientific crisis.²⁰ Ioannidis provides additional retrospective and commentary in his 2019 article.²¹

Statistical methodology in the sciences has been thoroughly scrutinized and critiqued in numerous papers. Greenland et al. (2016) thoroughly discuss the widespread misinterpretation of of statistical tests, confidence intervals, and statistical power, arguing that these statistics require high cognitive demands from scientists.²² In a 2016 statement on behalf of the American Statistical Association (ASA), Wasserstein and Lazar acknowledge that the misuse of p-values and the overreliance on the “p<0.05” threshold have led to widespread misinterpretations of statistical significance.²³ Benjamin et al. (2018) propose requiring p<0.005 as the default cutoff for new discoveries.²⁴ Amrhein, Greenland, and McShane call for abandoning the concept of statistical significance entirely, suggesting that researchers should focus on effect sizes, uncertainty intervals, and scientific reasoning instead of binary p-value thresholds.²⁵ In particular, they argue that more than half of surveyed scientists misinterpret large p-values as no effect. Pashler and Harris ask Is the replicability crisis overblown?²⁶

Meta studies and empirical findings.

On the topic of publication bias, Fanelli showed that the proportion of papers reporting null or negative results has been decreasing over time across most disciplines and countries, implying a publication bias toward positive results in the scientific literature.²⁷ Franco, Malhotra, and Simonovits tracked 221 social science experiments from design to publication and found that null findings are rarely published or are distorted as significant, empirically confirming the “file drawer” problem of unpublished null results.²⁸ Head et al. estimated the extent and consequences of p-hacking in science through textual analysis of scientific papers.²⁹ More broadly, John, Loewenstein, and Prelec survey over 2,000 psychologists and find a prevalence of questionable research practices, such as selective outcome reporting and data peeking.³⁰ Begley and Ellis (2012) discuss the replication crisis in cancer research, state that biotechnology firm Amgen succeeded in replicating published findings only in 11% of the cases.³¹

Goodhart’s law has been studied in the context of machine learning in the area called strategic classification.³² There are numerous reported instances of Goodhart’s law in various real-world policy problems. In particular, many papers have demonstrated and analyzed the discontinuity of p-values in different settings.³³ The discontinuity is not necessarily a sign of false positive findings. A contributing factor is also the file drawer effect that researchers don’t attempt to publish papers without significant findings.³⁴

On the topic of replication, I highlighted the Open Science Collaboration above that attempted to replicate 100 published psychology results.³⁵ I plotted the replication figure from the updated dataset available at osf.io/yt3gq (last modified: September 28, 2023). It is similar but not identical to the main figure of the original Science paper from 2015.

There are several other important replication studies. For example, Camerer et al. replicate 18 economics laboratory experiments published in top journals and find that 11 (61%) replicate successfully in the same direction, suggesting that many economic findings are robust but a substantial share fail to replicate.³⁶ In another study, Camerer et al. conduct replications of 21 high-profile social science experiments originally published in Nature or Science between 2010 and 2015 and find that 13 replications (62%) succeed, with replication effect sizes about half the magnitude of the originals on average.³⁷ In another meta study, Ioannidis, Stanley, and Doucouliagos analyzed 64,076 effect size estimates from 159 economics studies and found median statistical power around 18%, with roughly 80% of reported effects exaggerated, highlighting publication bias and low replicability in economics.³⁸ A major effort to replicate Brazilian biomedical research found that fewer than half of the experiments replicated.³⁹

Proposals for scientific reform.

There have been many calls for scientific reform. Munafò et al. issue a broad manifesto for reproducible science outlining steps to improve research reliability, including preregistration of studies, open sharing of data and code, routine replication, and incentive reforms to address the causes of irreproducible results.⁴⁰ Miguel et al. advocate for transparency in social science by adopting practices such as pre-analysis plans, open data, and replication studies (similar to medical trial standards), aiming to realign researchers’ incentives with producing credible, reproducible results.⁴¹ Kasy writes about the problem in the context of economics.⁴² Andrews and Kasy propose a method for identifying and correcting for publication bias.⁴³

In a popular audience book on the replication crisis, Clayton’s Bernoulli’s fallacy: Statistical illogic and the crisis of modern science makes the case for Bayesian reasoning to counter the crisis. Many have called for a shift to Bayesian methods along similar lines. Others have pointed out that Bayesian methods aren’t immune to the analog of p-hacking.⁴⁴

References

---

1. Open Science Collaboration, “Estimating the Reproducibility of Psychological Science”.↩︎

2. Goodman and Greenland, “ASSESSING THE UNRELIABILITY OF THE MEDICAL LITERATURE”; Goodman and Greenland, “Why Most Published Research Findings Are False”; Jager and Leek, “Empirical Estimates Suggest Most Published Medical Research Is True”.↩︎

3. Meehl, “Clinical Versus Statistical Prediction”; Dawes, Faust, and Meehl, “Clinical Versus Actuarial Judgment”.↩︎

4. Simmons, Nelson, and Simonsohn, “False-Positive Psychology”.↩︎

5. Center for Open Science, “Surpassing 100,000 Registrations on OSF”.↩︎

6. Gelman and Loken, “The Garden of Forking Paths”.↩︎

7. Gelman and Loken.↩︎

8. Gelman and Loken.↩︎

9. Tukey, “We Need Both Exploratory and Confirmatory”; Box, “Scientific Method”.↩︎

10. Goodhart and Goodhart, Problems of Monetary Management.↩︎

11. Gigerenzer et al., The Empire of Chance.↩︎

12. Simon, “Statistical Tests as a Basis for ‘Yes-No’ Choices”.↩︎

13. Morrison and Henkel, The Significance Test Controversy.↩︎

14. Meehl, “Theory-Testing in Psychology and Physics”.↩︎

15. Meehl, “Theoretical Risks and Tabular Asterisks”.↩︎

16. Meehl et al., “The Problem Is Epistemology, Not Statistics”.↩︎

17. Ioannidis, “Why Most Published Research Findings Are False”.↩︎

18. Simmons, Nelson, and Simonsohn, “False-Positive Psychology”.↩︎

19. Gelman and Loken, “The Garden of Forking Paths”.↩︎

20. Stark and Saltelli, “Cargo-Cult Statistics and Scientific Crisis”.↩︎

21. Ioannidis, “What Have We (Not) Learnt from Millions of Scientific Papers with p Values?”↩︎

22. Greenland et al., “Statistical Tests, p Values, Confidence Intervals, and Power”.↩︎

23. Wasserstein and Lazar, “The ASA Statement on p-Values”.↩︎

24. Benjamin et al., “Redefine Statistical Significance”.↩︎

25. Amrhein, Greenland, and McShane, “Scientists Rise up Against Statistical Significance”.↩︎

26. Pashler and Harris, “Is the Replicability Crisis Overblown? Three Arguments Examined”.↩︎

27. Fanelli, “Negative Results Are Disappearing from Most Disciplines and Countries”.↩︎

28. Franco, Malhotra, and Simonovits, “Publication Bias in the Social Sciences”.↩︎

29. Head et al., “The Extent and Consequences of p-Hacking in Science”.↩︎

30. John, Loewenstein, and Prelec, “Measuring the Prevalence of Questionable Research Practices with Incentives for Truth Telling”.↩︎

31. Begley and Ellis, “Raise Standards for Preclinical Cancer Research”.↩︎

32. Hardt et al., “Strategic Classification”.↩︎

33. Masicampo and Lalande, “A Peculiar Prevalence of p Values Just Below. 05”; De Winter and Dodou, “A Surge of p-Values Between 0.041 and 0.049 in Recent Decades (but Negative Results Are Increasing Rapidly Too)”; Ridley et al., “An Unexpected Influence of Widely Used Significance Thresholds on the Distribution of Reported p-Values”; Brodeur et al., “Star Wars”; Gerber and Malhotra, “Publication Bias in Empirical Sociological Research”.↩︎

34. Dwan et al., “Systematic Review of the Empirical Evidence of Study Publication Bias and Outcome Reporting Bias”.↩︎

35. Open Science Collaboration, “Estimating the Reproducibility of Psychological Science”.↩︎

36. Camerer et al., “Evaluating Replicability of Laboratory Experiments in Economics”.↩︎

37. Camerer et al., “Evaluating the Replicability of Social Science Experiments in Nature and Science Between 2010 and 2015”.↩︎

38. Ioannidis, Stanley, and Doucouliagos, “The Power of Bias in Economics Research”.↩︎

39. Initiative et al., “Estimating the Replicability of Brazilian Biomedical Science”.↩︎

40. Munafò et al., “A Manifesto for Reproducible Science”.↩︎

41. Miguel et al., “Promoting Transparency in Social Science Research”.↩︎

42. Kasy, “Of Forking Paths and Tied Hands”.↩︎

43. Andrews and Kasy, “Identification of and Correction for Publication Bias”.↩︎

44. Simonsohn, “Posterior-Hacking”.↩︎